堆
堆的概览
在这篇文章中,将会对c++中的stl容器中的堆进行一个讲解,主要讲解堆的概念,堆的使用,模拟堆,堆排序和优先队列这些内容
堆的概念
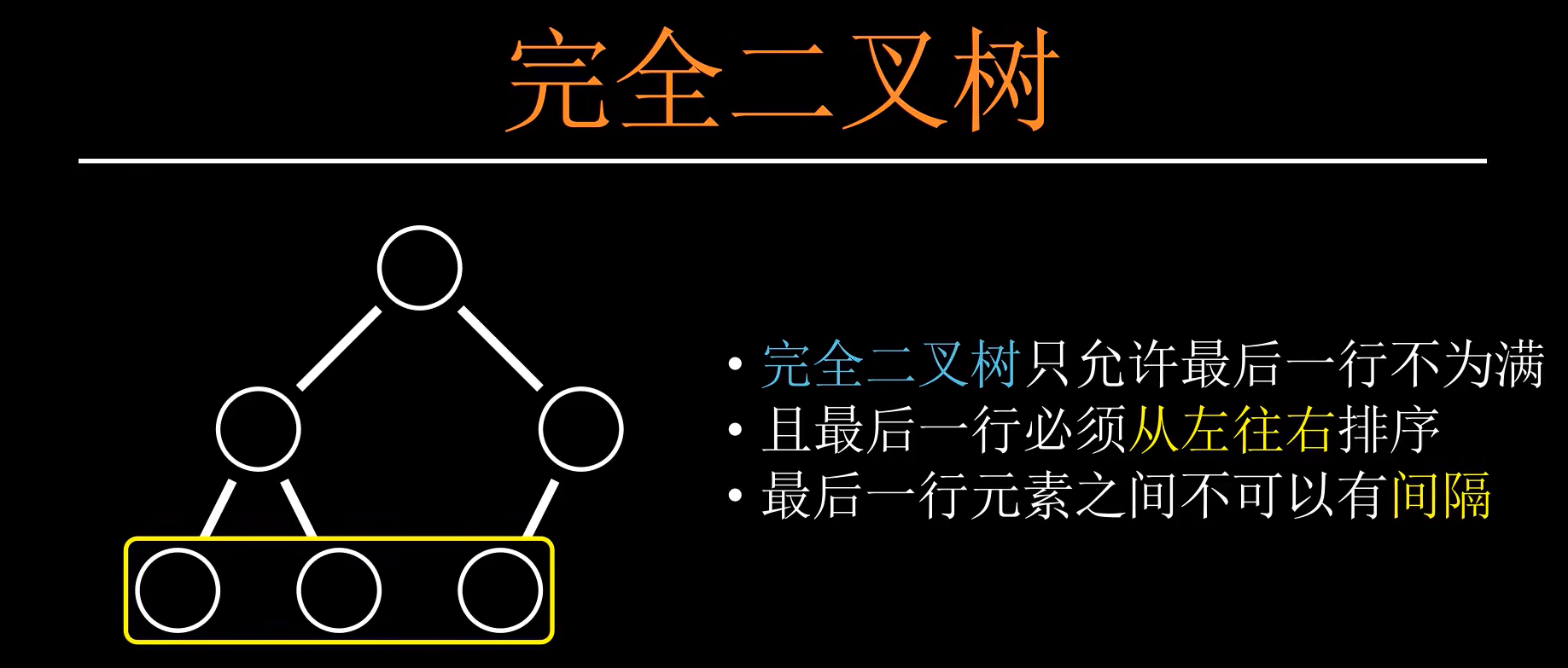
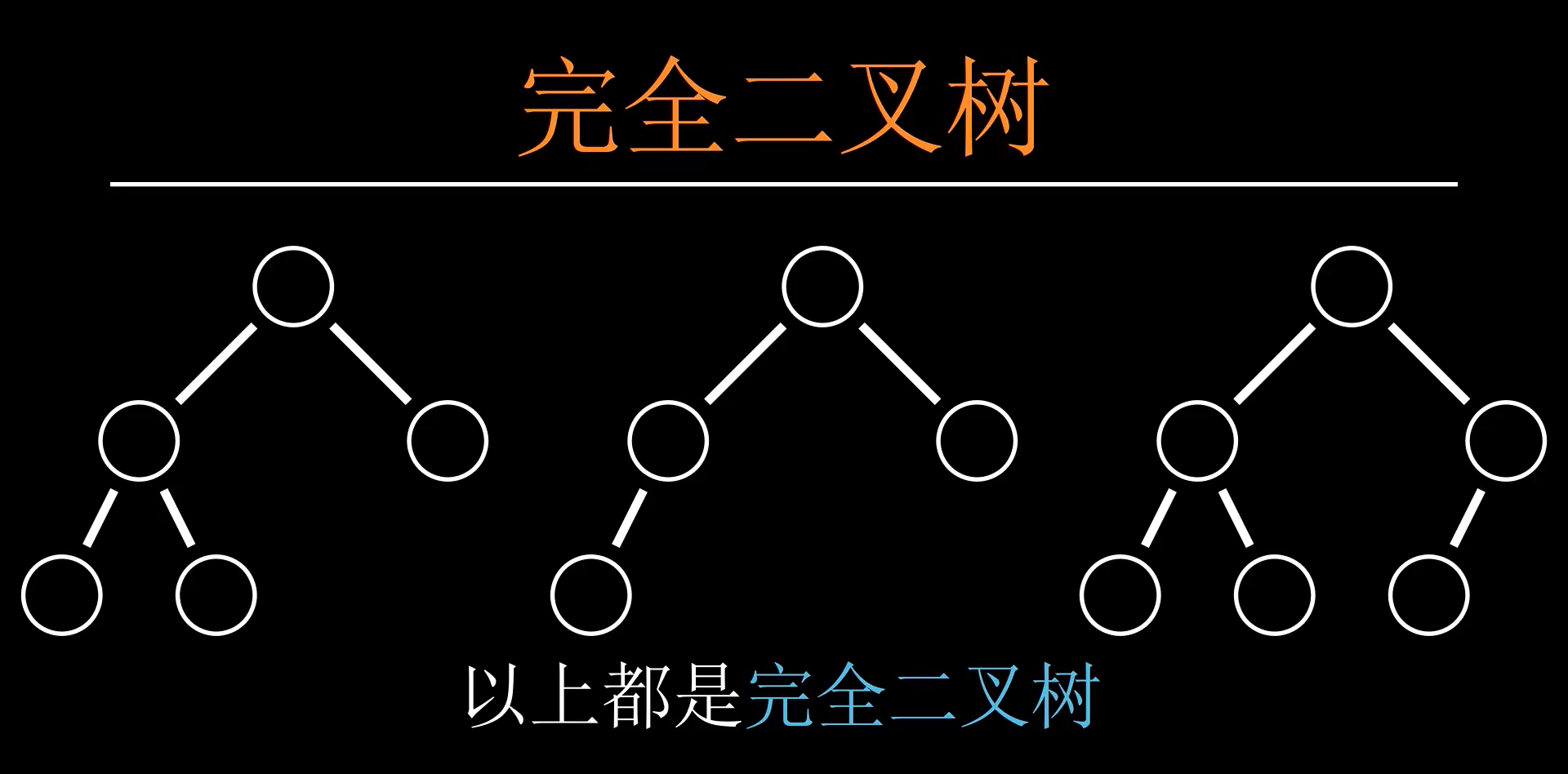
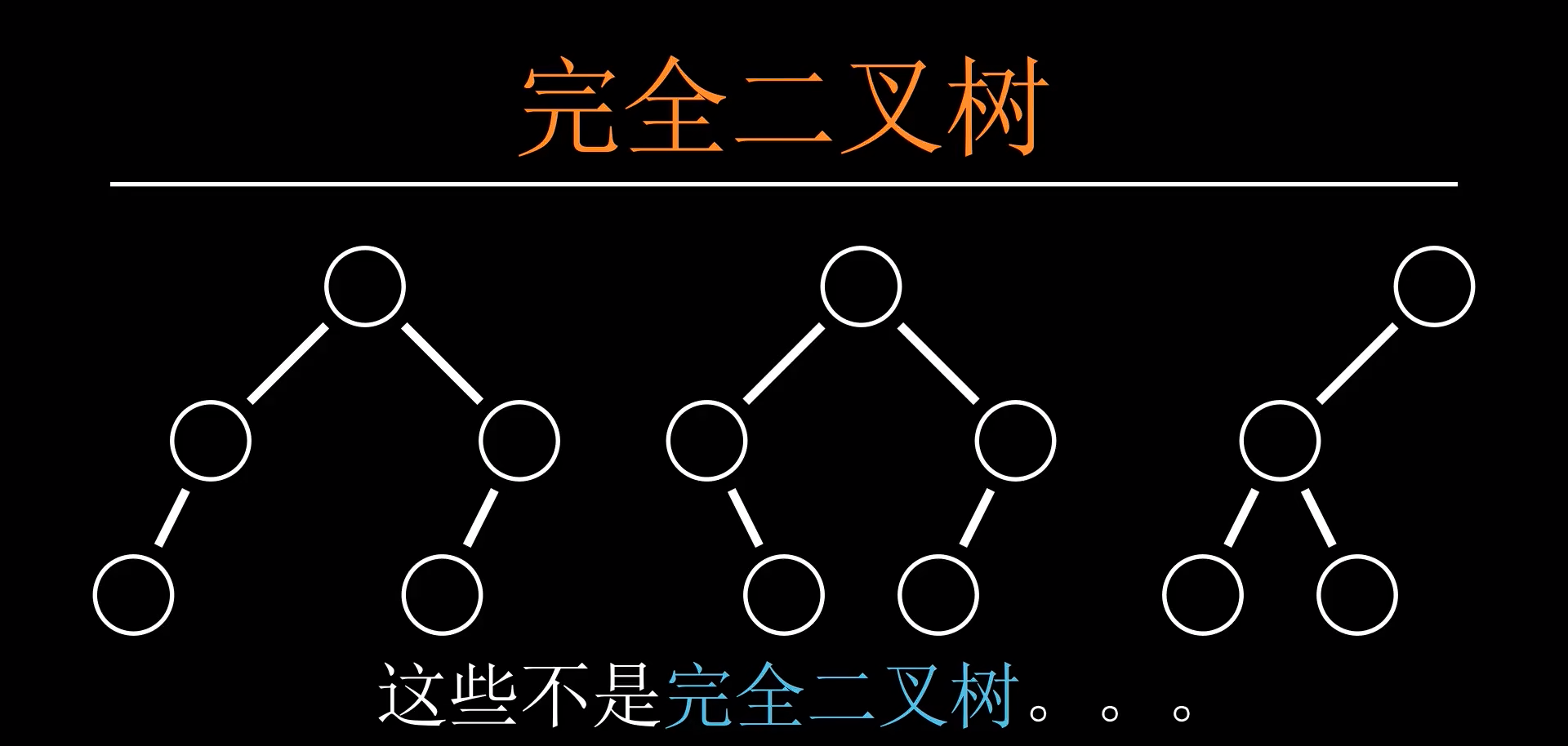
堆的本质实际上是一个完全二叉树,怎样才算是一个完全二叉树呢?
以下这些便是完全二叉树
非完全二叉树
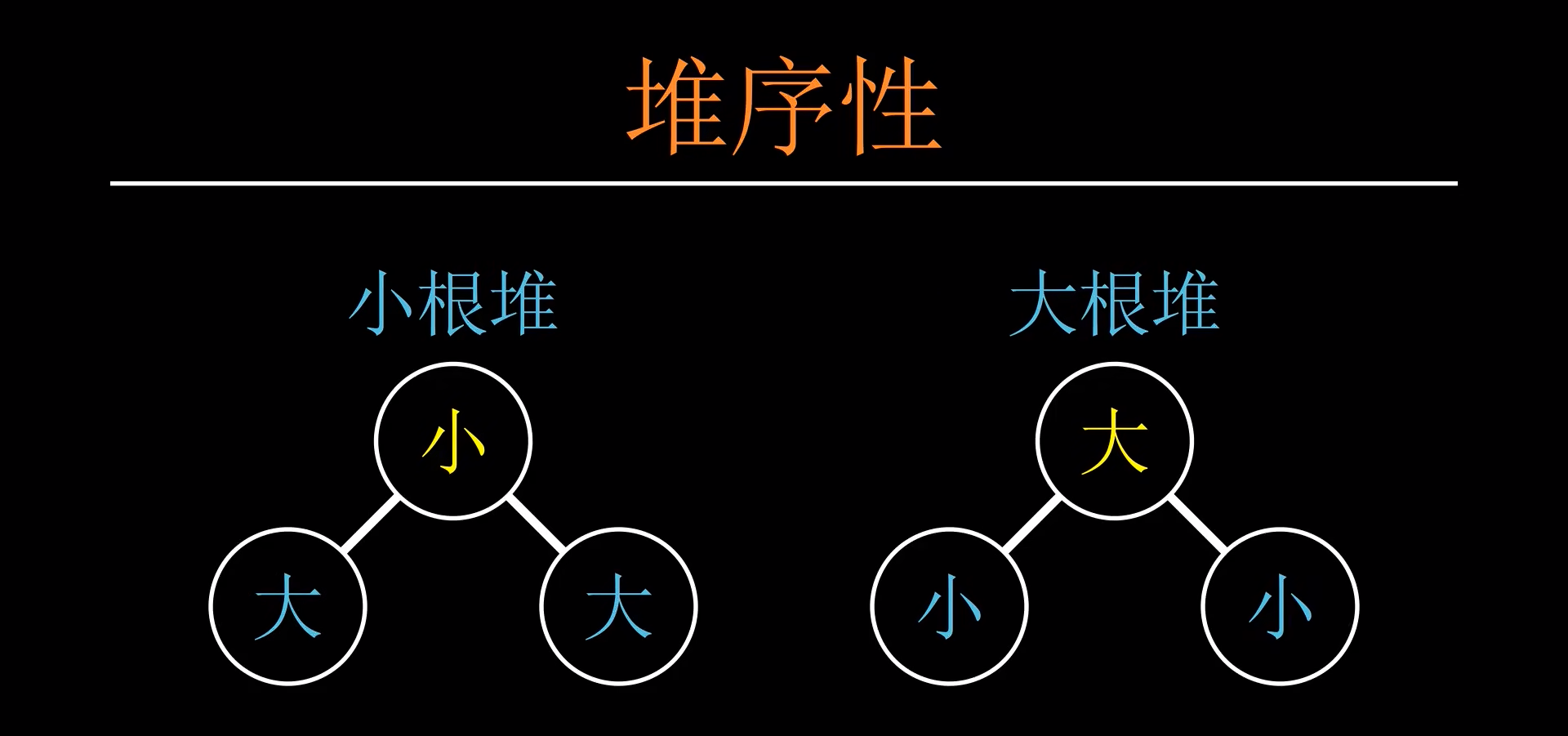
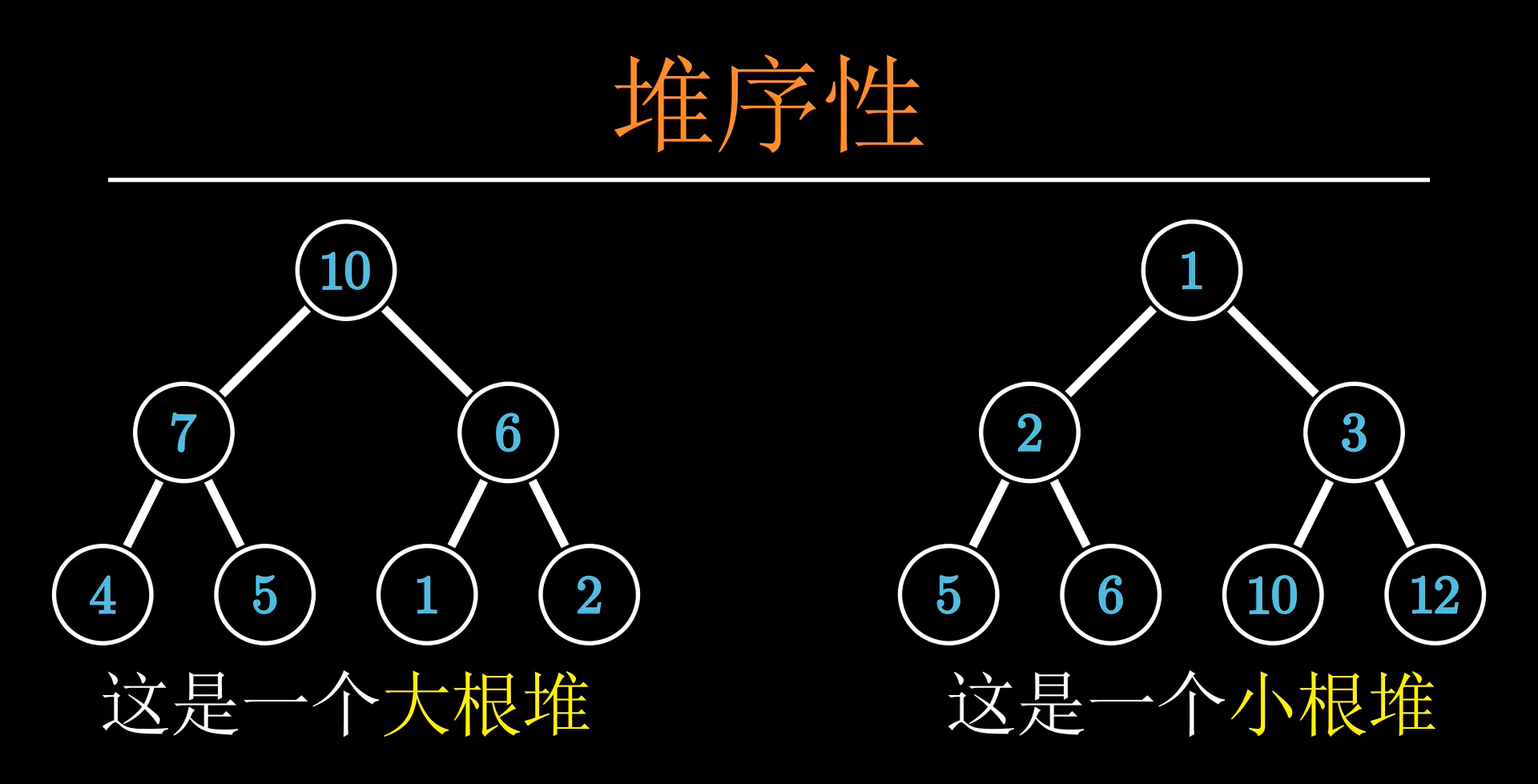
堆的堆序性
堆分为两种类型,第一种是大根堆,第二种是小根堆
小根堆,顾名思义,就是指在每一棵二叉树中,父节点都要比它的两个子节点要小,而所有点连起来的最上面的祖父节点就是最小的,
大根堆就是与小根堆完全相反的两个事物,在这里就不多做赘述了
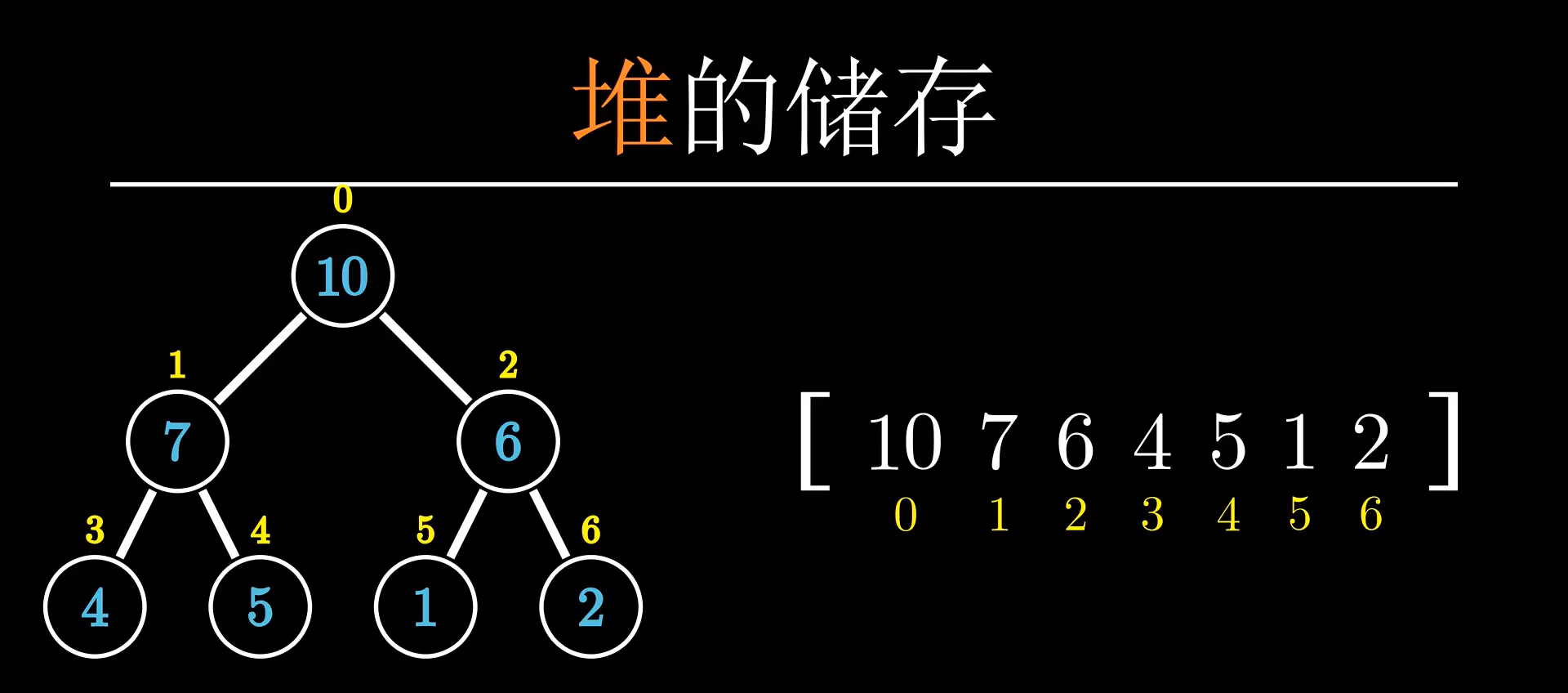
堆的储存
首先,我们可以按照层序遍历的顺序来给堆里面的元素编号 (层序遍历就是一层层的往下走,类似于宽度优先搜索)
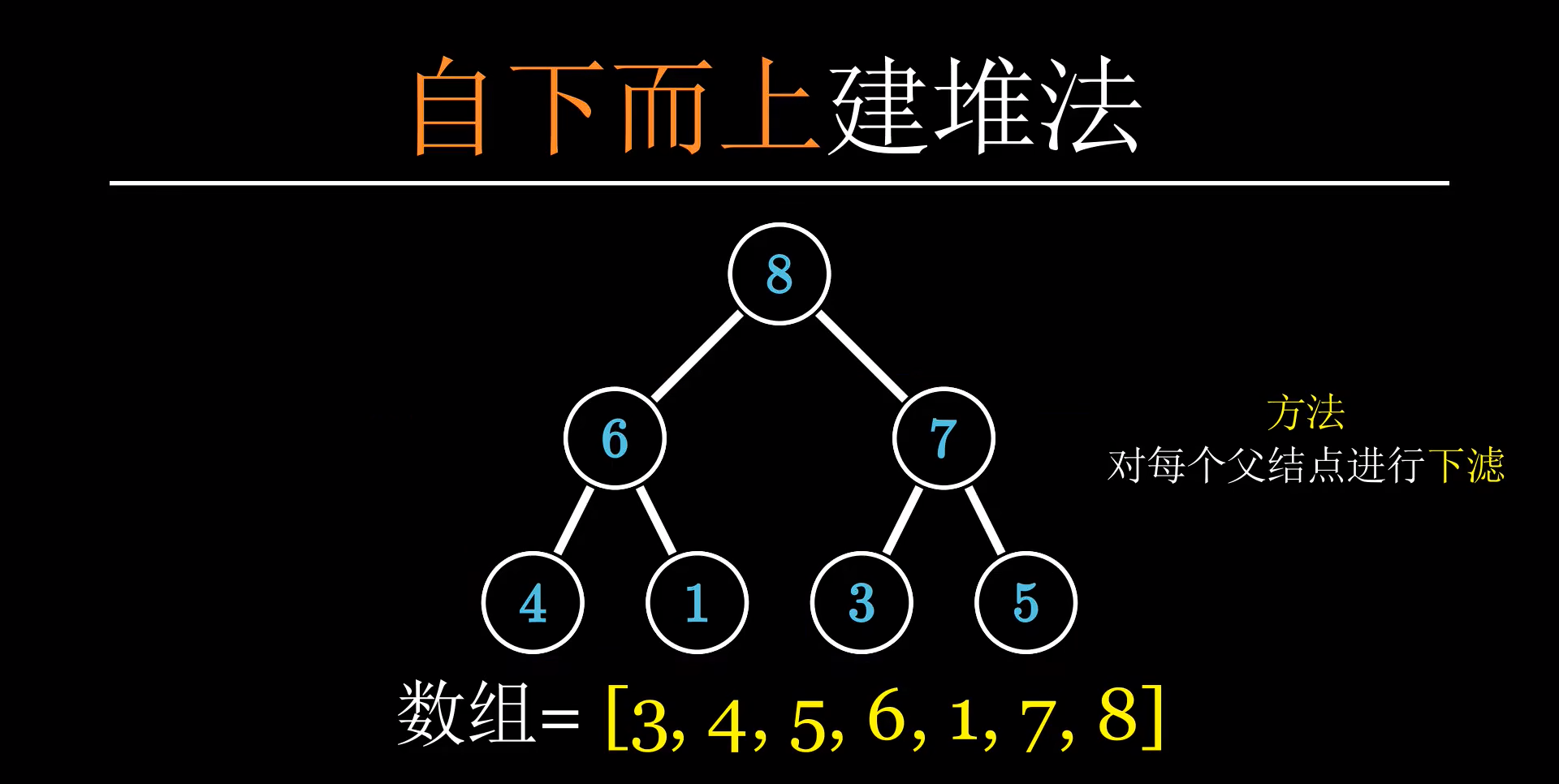
由于堆的层数是与编号是一一对应的,所以我们可以将一个堆通过使用一个一维数组的方式来实现
用一个父节点的位置找到子节点位置的方式就是通过数学规律来实现的,如这样2*n+1和2*n+2,便是上图中父节点找到子节点的一种方式
但是在竞赛中为了更加方便,一般情况下是将自顶而下的第一个父节点对应到一维数组中的第二个位置,这样的话,每一个父节点查找子节点的方式就改为了2*n和2*n+1
堆的基本操作
第一种是上滤,用函数表示的话就是up[x],第二种是下滤,用函数表示的话就是down[x],上滤是什么意思呢?我们在建造一个堆的时候,我们会涉及到堆的堆序性,也就是大根堆和小根堆的判断
我们以一张图来说明我们关于上滤和下滤的操作流程
首先,我们可以知道目前这个完全二叉树不是有序的,现在假设我们要将现在这个二叉树变成一个小根堆的形式
关于规则,我们假设加[]的是排好了序的,{}是没有排好序的
目前这个二叉树用一维数组表示的话是这样的{1 7 6 4 5 1 2}
现在这个二叉树有7个节点(包括根结点),我们在恢复成小根堆二叉树的时候只需要从倒数第二排的最后一个节点开始就行了,现在我们从6那个数的位置开始,让它与它的子节点进行比较。6比1大,也比2大,那么我们应该让6和谁换位置呢?
我们让6和1换位置,现在根节点的右子树变成了[1 6 2]
[1 6 2]现在是一个规范的右子树了,它满足了小根堆的性质
那如果我们让6和2换位置呢?那么右子树就会变成{2 1 6}这样的,它不满足小根堆的性质(2比1要大,按道理应该让1在右子树上的父节点),所以我们在换位置的时候还要选择与谁换位置
接下来是对于祖父节点上的二叉树的判断了,祖父节点上的二叉树用一维数组表示是{1 7 1},我们要看左边的7的位置是否正确,左子树上的元素是{7 4 5},不满足小根堆的要求,所以我们要让7和4交换
现在这个二叉树用一维数组表示的话是{1 4 1 7 5 6 2}
现在的话,这个二叉树就是用小根堆的形式呈现出来的二叉树了
下滤和上滤的代码如下
u指的是现在所处于的父节点,h[]是模拟堆形成的一个一维数组
void down(int u)
{
int t = u;
if (u * 2 <= idx && h[u * 2] < h[t]) t = u * 2;
if (u * 2 + 1 <= idx && h[u * 2 + 1] < h[t]) t = u * 2 + 1;
if (u != t)
{
swap(h[u], h[t]);
down(t);
}
}
void up(int u)
{
while (u / 2 && h[u / 2] > h[u])
{
swap(h[u / 2], [u]);
u /= 2;
}
}
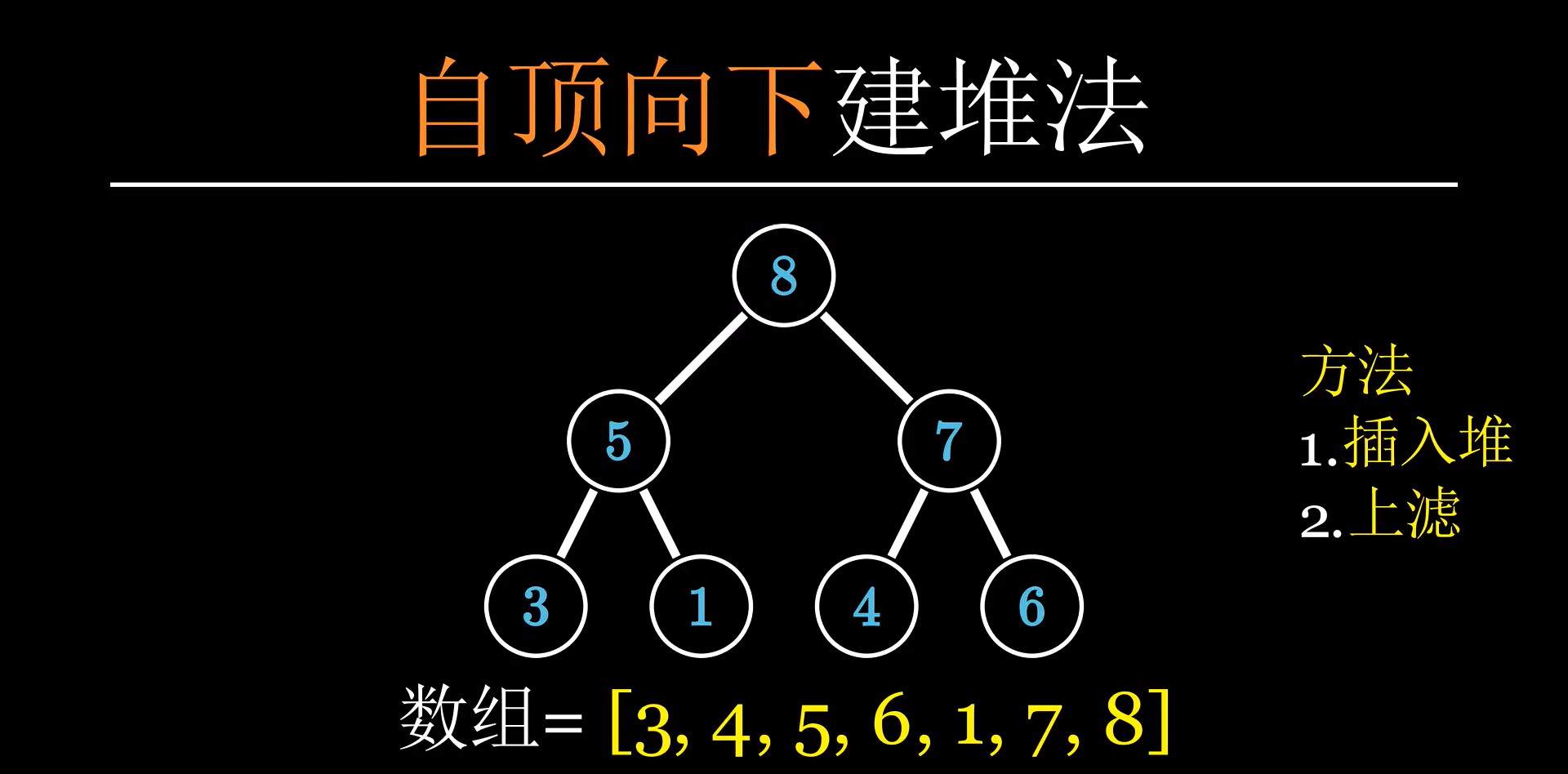
建堆方法
一共分为两种方式建一个堆,第一种是自顶而下建堆,第二种是自下而上建堆
自顶而下建堆就跟我们刚刚讲过的上滤操作相关
而自下而上建堆的话,就跟我刚刚讲过的下滤操作有关
优先队列
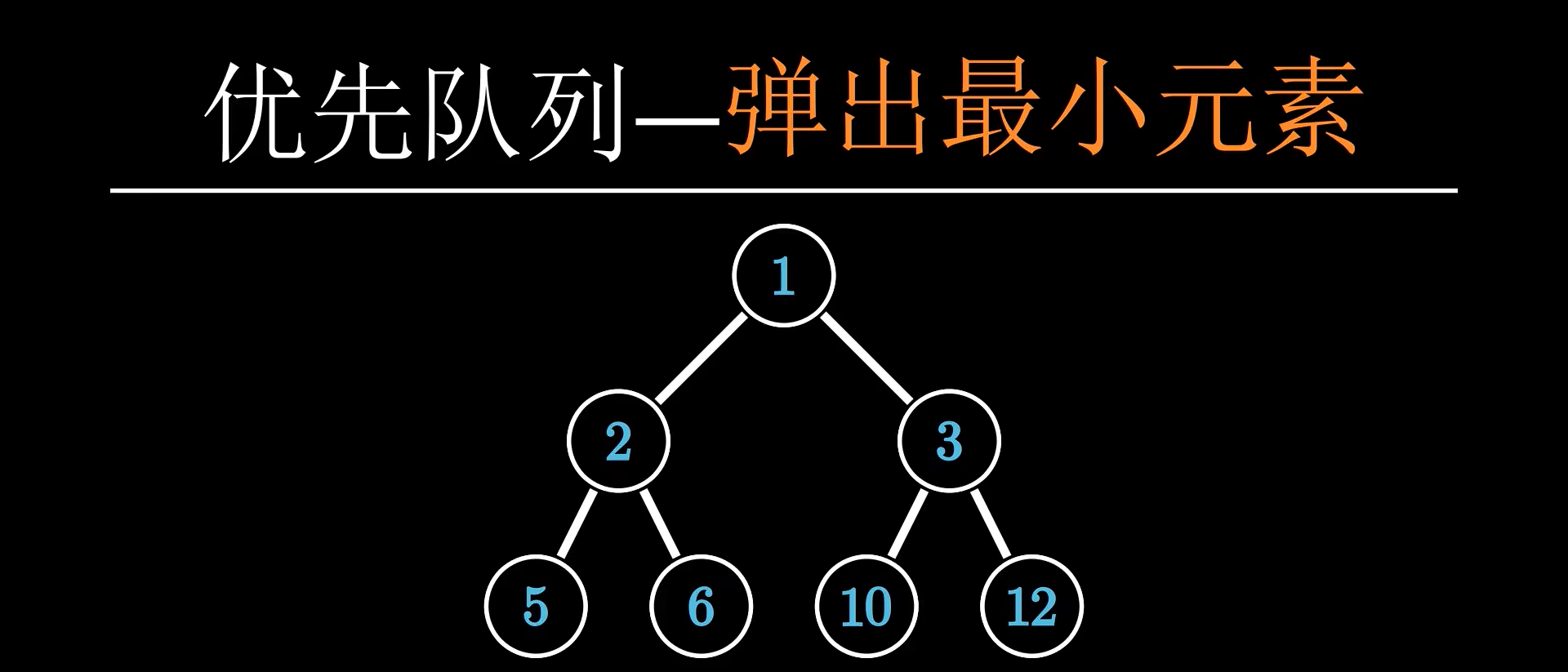
优先队列可以在堆排序算法中使用,普通的队列(队列的概念详见c++中的stl算法)是谁先进去,谁就先出来,优先队列不太一样(毕竟在名字上就已经体现出它的特殊性了),优先队列是谁先进去,但是要按照一定的顺序出来,比如说从大到小的顺序和从小到大的顺序这样子
我们来按照要求依次弹出最小的元素,但是堆的性质却不让我们这么做(堆只能一次次弹出头节点),那我们只好换个方式来做了
你们有没有玩过刺客信条?刺客在刺杀别人的时候是先刺杀最后一个人才不会被前面的人看见,如果我们直接去刺杀第一个人,那就不是刺杀了,是光明正大的杀人啊,所以为了将头元素取出来,我们要先把头节点放到最后一个节点上去,再把最后一个节点删掉,然后对头节点实行下滤down[x],这样我们就可以从小到大依次删除每一个元素了
idx指的是我们现在在所谓的堆上有多少个树(被删除的数都在数组后面)
swap(h[1], h[idx]);
[idx]--;
down(1);
优先队列的使用
自定义顺序的优先队列:
1.按从小到大顺序
priority_queue<int, vector<int>, greater<int> > heap;
2.按从大到小排序
priority_queue<int, vector<int>, less<int> > heap;
普通的优先队列:
1.按从大到小排序
priority_queue<int> heap;
特殊的优先队列:
1.必须要重载运算符
priority_queue<node> heap;
优先队列中的函数使用
取出队列中最高优先级的元素
heap.top()
删除队列中的目前最高优先级的元素
heap.pop()
计算队列中目前一共有多少个元素
heap.size()
插入一个元素到队尾的同时将队列按顺序排序
heap.push()
在优先队列中构造元素
heap.enplace()
判断优先队列内是否有元素
heap.empty()
与其他容器交换元素
heap.swap()
堆排序
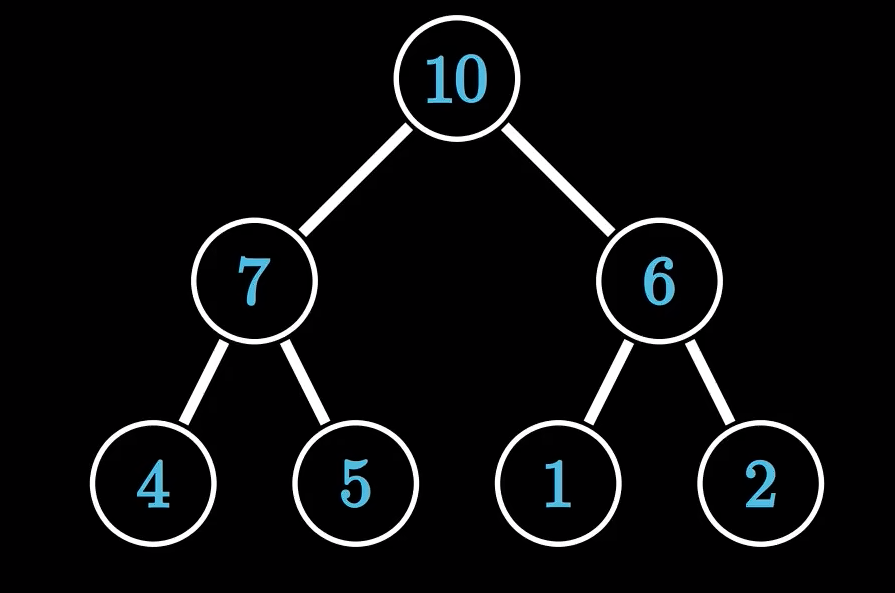
我们会发现,上面的优先队列把所有的点全部都弄出去了,但是呢,实际上我们不需要真的把点给丢弃掉,我们是把那些点依旧放在了数组里面,便于之后对于题目所处的问题进行一个及时的答复
这是一开始的大根堆,我们要对它的头节点进行一个删除处理
实际上,我们不是真的删除了头节点,只是把它给移到了下面去
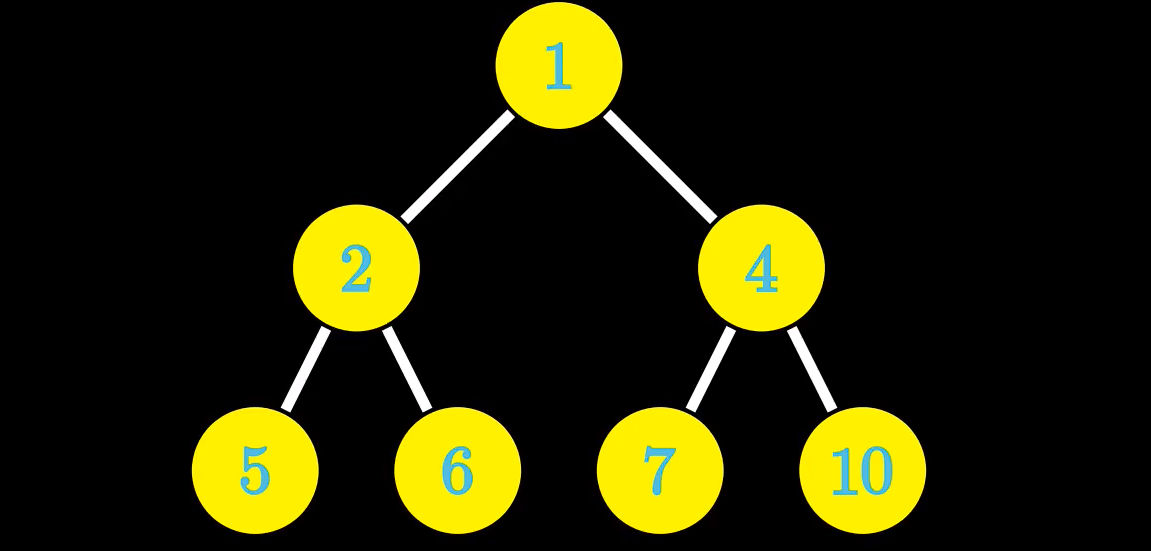
无序堆变成有序堆(实战)
我们先给堆里面添加元素,之后从第n/2个节点开始依次采用down[],使得一个无序堆变成一个有序的小根堆
代码如下:
int main()
{
cin >> n >> m;
int i;
for (i = 1; i <= n; i++) cin >> h[i];
idx = n;
for (i = n / 2; i; i--) down(i);
while (m--)
{
printf("%d ", h[1]);
h[1] = h[idx], idx--, down(1);
}
return 0;
}
结尾的话
首先,希望个位如果看到有什么错误的地方,或者说对于某些语句有更好的解释的话,烦请告知我(qq1594463152),我看到后会立刻修改自己的错误和错误的思考方向
另外,如果你用心看到这里的话,相信你一定可以学有所获!不过多多练习才是最重要的哦
引用
我这些图片一部分是来自于b站的up主制作的一个视频里面的截图,如有侵权等问题请立刻联系我,我立刻删除相关文章
引用视频网址如下