最短路问题(dijkstra算法)
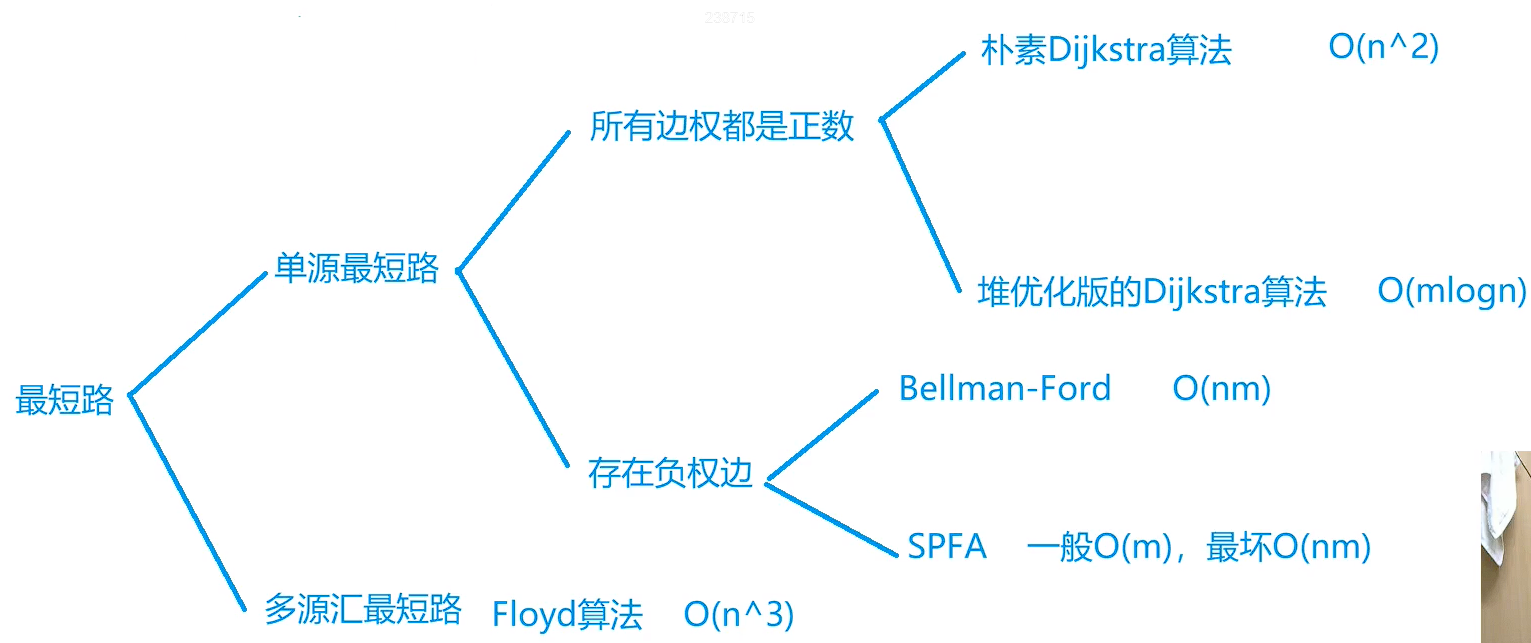
最短路问题的几种基本形式
我们约定俗成这样的惯例,在今后遇到最短路问题的时候,n是格子数,m指的是行数
在学习最短路算法的时候,我们主要学习的是图论中的代码的实现,而不是侧重于对代码的证明
小细节
稀疏图用堆优化,稠密图用朴素算法,负权边多用spfa
边数分析的情况下,边数很多时,稠密图用邻接矩阵,稀疏图用邻接表来存
最短路只考虑有向图的应用,无向图是一种特殊的有向图
有向图的意思是指两个点是有指向性的,就比如说有两个点a,b,a点指向b点,这就是指向性
而无向图的意思就是指a和b之间是没有指向性的,那我们就可以人为的进行指向性判断,我们让它们两个互相指向,这样的话不就相当于没有指向性了吗?(嘿嘿(●ˇ∀ˇ●))
朴素dijkstra算法
现在我们来介绍一下最短路问题中的第一种单源最短路算法,它的典型例题是这样的
1.例题
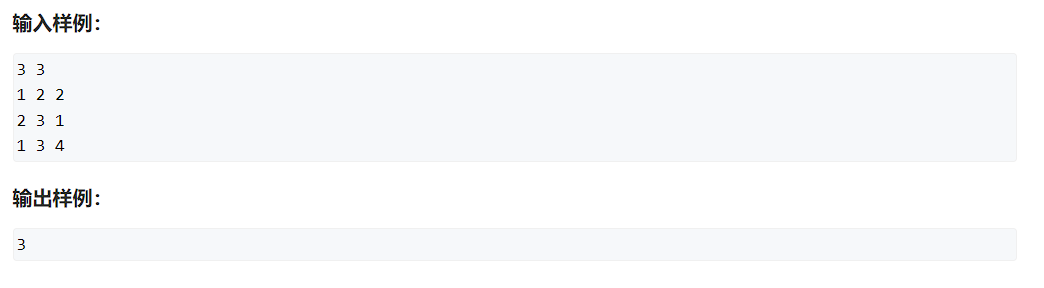
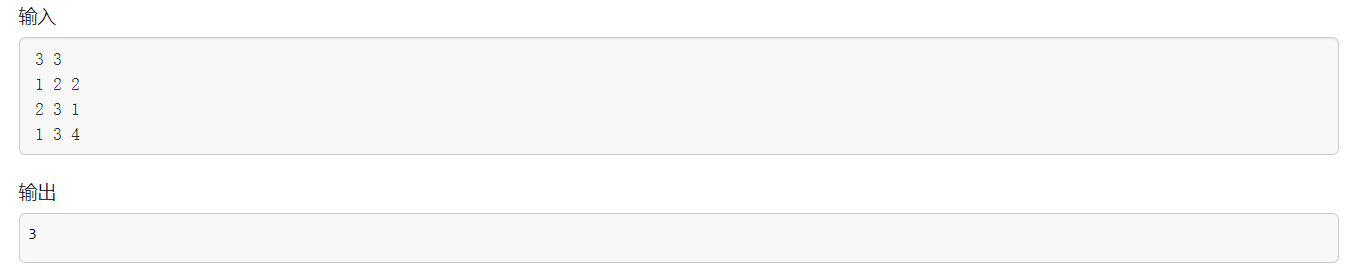
给定一个 n 个点 m 条边的有向图,图中可能存在重边和自环,所有边权均为正值。
请你求出 1 号点到 n 号点的最短距离,如果无法从 1 号点走到 n 号点,则输出 −1
1.1.输入格式
第一行包含整数 n 和 m。
接下来 m 行每行包含三个整数 x,y,z,表示存在一条从点 x 到点y 的有向边,边长为z
1.2输出格式
输出一个整数,表示 1 号点到 n 号点的最短距离。
如果路径不存在,则输出 −1
题目解释和算法构建
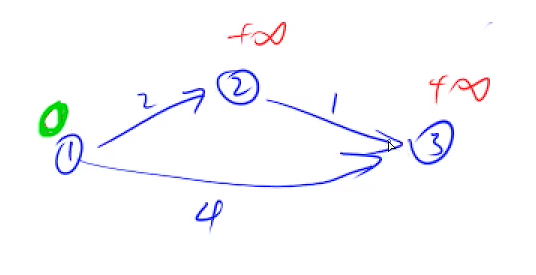
这道题的意思是说,我们有三个点,三条边(在这道例题里面是没有无向边的说法的),第一次我们连了1和2,第二次我们连了2和3,第三次我们连了1和3,图像长这样
我们现在要输出最短路的距离,我来说一个小故事吧
1.过桥
记得在小学的时候我们学习过一种规划时间的方法,比如说我现在要做一个番茄炒鸡蛋,要打鸡蛋,洗番茄,煮米饭,炒菜,它们的时间不同,我们该怎么用最短的时间完成所有的方案后顺利吃到我们想要的菜呢?这时候就需要合理的规划时间了
同时,我们看上面的这幅图是不是很像三座桥,2 1 4就是我们过桥所需要的时间,现在我们想知道,当我们从第一座桥出发,到最后一座桥需要的最快时间是多少。用肉眼我们可以很快的知道答案是3。但是电脑不知道,这时候就需要我们设计算法了。
小思考
我们思考一下,从第一座桥出发,第一座桥到第一座桥需要多长时间呢?(这不很简单嘛,作者怎么会问这么智障的问题???),答案是0,我们就在桥的上面,现在我们的第一座桥连着哪些桥呢?连着2号桥和3号桥,我们看看第二座桥和第三座桥分别到第一座桥的时间分别是2和4,如果是你,你想要快点到终点,你会选择哪座桥呢?
答案无疑是2号桥,现在我们去到2号桥吧
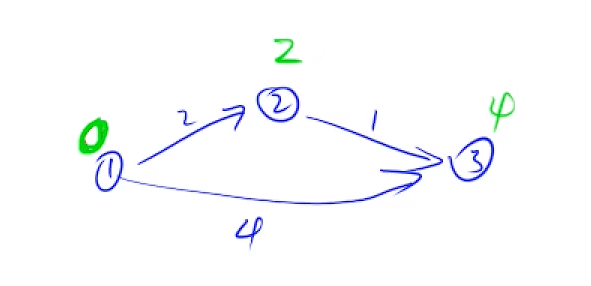
2.第二座桥
我们来到了2号桥,2号桥连接着哪些桥呢?(连着1号和3号,这不显而易见嘛(●ˇ∀ˇ●)),我们刚刚走过了1号桥了,总不可能再走一次1号桥了吧,所以我们去分析3号桥,3号桥离2号桥的距离是1,2号桥离1号桥的距离是2,这时候我们去到3号桥就有了两种情况,一种要走3步,一种要走4步,为了更快的到达终点,我们选择走3步的,这时候3号桥的距离被刷新成3了,这样一来我们也找到了最快过桥方案
[说明图如下]
算法实现
1.初始化距离(只有起点距离确定),dist[1]=0,dist[i] = 极大的数(因为我们并不知道要多大)
2.for循环,循环n次
2.1已确定最短距离的点s,找到不在s中的距离最近的点t
2.2把t加到s中去
2.3用t更新其它点的距离dist[x]>dist[t]
1.重边和闭环
重边(1,2)与闭环(1)
重边就是自己修了两条走向同一个位置的桥
闭环就是自己修了一条走向自己的桥
重边:只要保留最短的那条边就可以了,g[a][b]=min(g[a][b],c),
代码实现
1.定义初始值
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510;
int n,m;
int g[N][N],dist[N];
bool st[N];int main()
{
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof(g));
while(m--)
{
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b] = min(g[a][b],c);
}
cout<<dijkstra()<<endl;
return 0;
}其中,n,m,a,b,c都是题目要求的输出变量
定义的bool变量st是用来看我们的桥有没有走过,g[][]是说明a号点与b号点相连接的桥的距离(无向边则表示的是相连的最小距离),dist变量指的是目前我们所处的这座桥到原点的最短距离
开始我们按照题目要求输入,开始把g数组的值放的很大,0x3f3f3f3f是一个很大的数了(为什么上面只写了0x3f呢,因为g是一个int变量,而0x3f所指的是char变量的,int变量是char变量的4倍,所以是0x3f3f3f3f)
2.进入dijkstra函数
理解的话,我们可以按照上面的算法构建和实现来理解,下面只是对理解形成代码的一种形式(也很重要)
这里面的i只要遍历n-1次就可以了,最后的不用遍历了
int dijkstra()
{
memset (dist, 0x3f, sizeof(dist));
dist[1] = 0;
int i, j;
for (i = 0;i < n - 1; i++)
{
int t = -1;
//从第一座桥开始遍历,知道找到离第一座桥最短的那座桥
for (j = 1; j <= n; j++)
{
//如果这座桥没有被遍历过&&(没有离开第一座桥 现在 所呆着的桥与原桥的位置 比 新找的桥与原桥的位置 大)
if (!st[j] && (t == -1 || dist[t] > dist[j]))
//更新现在所待的桥
t = j;
}
//从新找的桥的位置开始,把其它没有走过的桥的 原桥到原点的距离 和原桥从我们现在处于的桥的距离与现出的桥到原点距离之和 比 较最小值
for (j = 1; j <= n; j++)
{
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
//走过的桥标记一下
st[t] = true;
}
if (dist[n] == 0x3f3f3f3f) return -1;
else return dist[n];
}3.输出结果
感想
从这一章节开始便是正式进入了最短路的这个系列的学习了,笔者也是学了一个知识点,总结之后便发表出来了,这里面可能会存在很多漏洞和未解释清楚的东西,如果有发现的话还请麻烦联系我(qq1594463152)更改内容(不能让这屑作毒害别人hhh)
引入
—acwing算法基础课 (yxc主讲)
堆优化版的dijstra算法
时间复杂度mlogn
实现堆:手写堆,或者优先队列stl算法
算法实现: 稀疏图,采用邻接表的形式进行(邻接表指的是多个单链表)
初始化
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
const int N = 1e6 + 10;
int n, m;
int h[N], w[N], e[N], ne[N], idx;
int dist[N];
bool st[N]; 在单链表专栏中我们有专门介绍e[N],ne[N],idx三个链表中变量的意思, e[N]的意思是保存数字用的,ne[N]是用来存储地址的,idx指的是队列(或列表)中一共有多少次链接
w[N]指的是我们每一条路的权重,就是说我们一给点到另外一个点所需要的权重值(也就是过桥所需要的时间),h[a]的意思是记录我们在进行链表存储中所需要的数值
在我们按照题目要求输入n,m后,便是我们的算法开始了
首先,作为邻接表,它的表头要首先初始化为空,便于我们后续的idx操作
我们要用一个堆来维护所有点的距离, 在维护所有距离的时候,我们还要知道相对的点的编号是多少, 因此我们要一个pair容器来存储
注意:用邻接表存储的时候有重复边也没有关系,我们的邻接表会一一记录下来的同时,会选择最小的那个边
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
while (m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
cout << dijkstra() << endl;
return 0;
}单链表操作
代码解释: 第一步是对b的数进行存储,说明a是与b有相连的
w是对权重的一个存储, ne操作便是给a这个位置添加一个新的单链
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}dijkstra算法代码实现
很多人可能不知道下面的一串较长的代码是怎么回事, 其实它就是优先队列里面的一种
详情见(c++中的stl算法—堆)
int dijkstra()
{
memset(dist, 0x3f, sizeof dist);
dist[1] = 0;
//定义一个优先队列
priority_queue<PII, vector<PII>, greater<PII>> heap;
//入队
heap.push({ 0, 1 });
while (heap.size())
{
//取出队列中的第一个最大优先级的元素
auto t = heap.top();
//删除队列中最大优先级的元素
heap.pop();
int ver = t.second, distance = t.first;
if (st[ver]) continue;
st[ver] = true;
for (int i = h[ver]; i != -1; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({ dist[j], j });
}
}
}
if (dist[n] == 0x3f3f3f3f) return -1;
return dist[n];
}dijkstra算法的优化1
(记录最短距离的同时记录边)
我们可以再次引入一个k数组,k数组的作用就是记录我们目前所在的点是由哪一个点更新的,那么我们该什么时候记录呢,很简单,就是在更新最短距离的时候就可以记录了,下面看代码!
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({dist[1], 1});
while(heap.size()) {
auto t = heap.top();
heap.pop();
int distance = t.first, div = t.second;
if(st[div]) continue;
st[div] = true;
for(int i = h[div];i != -1;i = ne[i]) {
int j = e[i];
//刷新最短路
if(dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
//记录此时是谁将它的最短路更新的
k[j] = div;
heap.push({dist[j], j});
}
}
}
return dist[n];
}现在,我们的k数组就可以记录最短边了,我们可以通过k数组的依次遍历找回初始点
//倒序输出从1号点到n号点的点
for(int i = n;i != 1;i = k[i]) {
//输出
cout << k[i] << ' ';
}但是呢,现在我们只能够记录初始点是怎么到结束点的,但是它们的两个点两个点直接的距离是怎么算的呢?请看!
我们每一次查询,都是再找是哪个k[i] 到达的i,但是邻接表上,我们在记录的点是被更新过的,这句话请看解释
解释
我们将两条边加入邻接表
1 3 5
1 2 6现在假设我们只有这两条边,我们加入第一条边的时候是这样的
idx = 0;
e[idx] = 3, w[idx] = 5, ne[idx] = h[1], h[1] = idx++;加入第二条边是这样的
idx = 1;
e[idx] = 2, w[idx] = 6, ne[idx] = h[1], h[1] = idx++;发现了没,我们的h[i],是被更新过的,所以我们是无法直接通过h[k[i]]查询k[i] -> i 的最小边的
所以我们要像dijkstra算法那样遍历我们的数组
for(int j = h[k[i]];j != -1;j = ne[j]) 当我们的e[j] == 我们的i的时候,此时我们就找到了最短的边了,但是呢,我们还要考虑到有重边的情况,就是说我们的k[i] -> i可能不止只有一条边,所以为了防止这种情况发生,我们需要计算出重边的最小值,这个就简单了
我们只需要添加这一步即可
//倒序输出从1号点到n号点的点
for(int i = n;i != 1;i = k[i]) {
//输出
cout << k[i] << ' ';
//输出k[i] -> i 号点的距离,直接对h[k[i]进行累退(推)即可
//定义一个minn变量记录最小值
int minn = 0x3f3f3f3f;
for(int j = h[k[i]];j != -1;j = ne[j]) {
//找到了i号点
if(e[j] == i) {
//刷新最小距离
minn = min(minn, w[j]);
}
}
//把k[i] -> i 号点的距离输出出来
cout << minn << endl;
}现在一来,我们就可以输出从1号点到达n号点的过程了,下面是代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1000010;
typedef pair<int, int> PII;
//k记录的是所有的点对应的最短路中的边
int dist[N], k[N];
int n, m;
int e[N], ne[N], idx, h[N], w[N];
bool st[N];
//邻接表
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({dist[1], 1});
while(heap.size()) {
auto t = heap.top();
heap.pop();
int distance = t.first, div = t.second;
if(st[div]) continue;
st[div] = true;
for(int i = h[div];i != -1;i = ne[i]) {
int j = e[i];
//刷新最短路
if(dist[j] > distance + w[i]) {
dist[j] = distance + w[i];
//记录此时是谁将它的最短路更新的
k[j] = div;
heap.push({dist[j], j});
}
}
}
return dist[n];
}
int main()
{
cin >> n >> m;
memset(h, -1, sizeof(h));
for(int i = 0;i < m;i++) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
}
int t = dijkstra();
//倒序输出从1号点到n号点的点
for(int i = n;i != 1;i = k[i]) {
//输出
cout << k[i] << ' ';
//输出k[i] -> i 号点的距离,直接对h[k[i]进行累退(推)即可
int minn = 0x3f3f3f3f;
for(int j = h[k[i]];j != -1;j = ne[j]) {
//找到了i号点
if(e[j] == i) {
//把k[i] -> i 号点的距离输出出来
minn = min(minn, w[j]);
}
}
cout << minn << endl;
}
return 0;
}输入:
8 14
2 5 5
1 2 1
2 3 2
3 1 3
2 5 4
1 2 3
3 5 1
3 4 3
4 5 5
5 7 4
5 6 7
6 8 3
4 7 9
7 8 2输出:(倒序输出的)
点 距离 //起至末(解释)
7 2 7 -> 8
5 4 5 -> 7
3 1 3 -> 5
2 2 2 -> 3
1 1 1 -> 2